import java.lang.*;
// Approach#1 O(n^6) time.
public class LargestSubmatrixSum {
// Given an NxN matrix of positive and negative integers, write code to find the
// submatrix with the largest possible sum.
//brute force: O(n^6) time.
//returns [r1, c1, r2, c2, sum] where (r1,c1),(r2,c2) represents
//the diagonal of submatrix
static int[] findLargestSubmatrix(int[][] matrix) {
int maxSum = Integer.MIN_VALUE;
int[] ret = {-1, -1, -1, -1, 0};
for (int r1 = 0; r1 < matrix.length; ++r1) {
for (int r2 = r1; r2 < matrix.length; ++r2) {
for (int c1 = 0; c1 < matrix[0].length; ++c1) {
for (int c2 = c1; c2 < matrix[0].length; ++c2) {
int sum = getSum(matrix, r1, c1, r2, c2);
if (sum > maxSum) {
maxSum = sum;
ret = new int[] {r1, c1, r2, c2, sum};
}
}
}
}
}
return ret;
}
static int getSum(int[][] matrix, int r1, int c1, int r2, int c2) {
int sum = 0;
for (int r = r1; r <= r2; ++r) {
for (int c = c1; c <= c2; ++c) {
sum += matrix[r][c];
}
}
return sum;
}
// Approach#1 O(n^4) time.
//preprocess matrix: O(n^4) time, reducing getSum to constant time.
static int[][] processMatrix(int[][] m) {
if (m == null) return null;
int[][] sumMatrix = new int[m.length][m[0].length];
sumMatrix[0][0] = m[0][0];
for (int j = 1; j < m[0].length;j++){
sumMatrix[0][j]=sumMatrix[0][j-1]+m[0][j];
//System.out.println(0+","+j+" - "+sumMatrix[0][j]+",");
}
for (int i = 1; i < m.length;i++){
sumMatrix[i][0]=sumMatrix[i-1][0]+m[i][0];
//System.out.println(i+","+0+" - "+sumMatrix[i][0]+",");
}
for (int i =1; i< m.length;i++) {
for (int j=1; j < m[0].length;j++){
sumMatrix[i][j] = sumMatrix[i-1][j]+sumMatrix[i][j-1]-sumMatrix[i-1][j-1]+m[i][j];
//System.out.println(i+","+j+" - "+sumMatrix[i][j]+",");
}
}
return sumMatrix;
//for (int i = 0; i < m.length; ++ i) {
// int sumRowOne = 0; int sumColOne = 0;
// for (int j = 0; j < m[0].length; ++j) {
// if (i == 0) {
// sumRowOne += m[i][j];
// sumMatrix[i][j] = sumRowOne;
// }
// if (j == 0) {
// sumColOne += m[i][j];
// sumMatrix[i][j] = sumColOne;
// }
// if (i != 0 && j != 0) {
// sumMatrix[i][j] = m[i][j] +
// sumMatrix[i][j-1] +
// sumMatrix[i-1][j] -
// sumMatrix[i-1][j-1];
// }
// System.out.println(i+","+j+" - "+sumMatrix[i][j]+",");
// }
//}
//return sumMatrix;
}
static int getSum2(int[][] sumMatrix, int r1, int c1, int r2, int c2) {
if (r1 == 0 && c1 == 0){
return sumMatrix[r2][c2];
}
else if (r1 == 0){
return sumMatrix[r2][c2]-sumMatrix[r2][c2-1];
}
else if (c1 == 0 ){
return sumMatrix[r2][c2]-sumMatrix[r1-1][c2];
} else {
return sumMatrix[r2][c2]-sumMatrix[r2][c1-1]-sumMatrix[r1-1][c2]+sumMatrix[r1-1][c1-1];
}
// return sumMatrix[r2][c2] -
// sumMatrix[r1][c2] -
// sumMatrix[r2][c1] +
// sumMatrix[r1][c1];
}
static int[] findLargestSubmatrix2(int[][] matrix) {
int maxSum = Integer.MIN_VALUE;
int[] ret = {-1, -1, -1, -1, 0};
int[][] subMatrix = processMatrix(matrix);
for (int r1 = 0; r1 < matrix.length; ++r1) {
for (int r2 = r1; r2 < matrix.length; ++r2) {
for (int c1 = 0; c1 < matrix[0].length; ++c1) {
for (int c2 = c1; c2 < matrix[0].length; ++c2) {
int sum = getSum2(subMatrix, r1, c1, r2, c2);
//System.out.println(r1+","+c1+";"+r2+","+c2+" - "+sum+",");
if (sum > maxSum) {
maxSum = sum;
ret = new int[] {r1, c1, r2, c2, sum};
}
}
}
}
}
return ret;
}
// Approach#3 O(n^3) time.
/**
*
* @param matrix
* @return return the max.
* 1,1,1 => row start
* 2,2,2
* + 3,4,5 => row end
* ________
* 6,7,8 => one row thinking => find maximum subarray?
* check every end and sum so far
* row =0 end => 1,1,1 => find maximum subarray?
* row =1 end => 3,3,3 => find maximum subarray?
* row =2 end => 6,7,8 => find maximum subarray?
*/
public static int maxSubMatrix(int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return 0;
}
int max = Integer.MIN_VALUE;
for (int start = 0; start < matrix.length; ++start) {//different row start form different submatrix
int[] arr = new int[matrix[0].length];// a new array for storing column compressing sum
for (int end = start; end < matrix.length; ++end) {// different end with same start form different submatrix
// Construct a array
for (int k = 0; k < matrix[0].length; ++k) {
arr[k] += matrix[end][k];
}
// Find maximum subarray
max = Math.max(max, maxArea(arr));
}
}
return max;
}
// use max subarray to find max
private static int maxArea(int[] arr) {
int local = 0;// NOTE: cannot Integer.MIN_VALUE
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length;i++){
local = Math.max(arr[i], local+arr[i]);
max= Math.max(local, max);
}
return max;
}
//--------------------------------------
public static void main(String[]args) {
int[][]m = {
{1,-2,3,1},
{1,5,-4,1},
{1,1,0,2},
{-1,1,1,-8}};
long start = System.nanoTime();
int[] r = findLargestSubmatrix(m);//// Approach#1 O(n^6) time.
long end = System.nanoTime();
System.out.println("Time:"+(long)(end-start)+"("+r[0]+", "+r[1]+") ("+r[2]+", "+r[3]+") sum: "+r[4]);
long start2 = System.nanoTime();
int[] r2 = findLargestSubmatrix2(m);//// Approach#2 O(n^4) time.
long end2 = System.nanoTime();
System.out.println("Time:"+(long)(end2-start2)+"("+r2[0]+", "+r2[1]+") ("+r2[2]+", "+r2[3]+") sum: "+r2[4]);
long start3 = System.nanoTime();
int r3 = maxSubMatrix(m);//// Approach#3 O(n^3) time.
long end3 = System.nanoTime();
System.out.println("Time:"+(long)(end3-start3)+", sum:"+r3);
}
}
[Old ]
1. ExampleArea(x2,y2,x1,y1) = Area(x2,y2) - Area(x1,y2)- Area(x2,y1) + Area(x1,y1)
sumMatrix[i][j] =
matrix[i][j] + sumMatrix[i - 1][j] + sumMatrix[i][j - 1] - sumMatrix[i - 1][j - 1] ;
if ( i==0 && j ==0 ) {
sumMatrix[i][j] = matrix[i][j];
}
else if ( j == 0 )
{
sumMatrix[i][j] = matrix[i][j] + sumMatrix[i-1][j];
}
else if ( i == 0 )
{
sumMatrix[i][j] = matrix[i][j] + sumMatrix[i][j-1];
}
else
{
sumMatrix[i][j] = matrix[i][j] + sumMatrix[i-1][j] + sumMatrix[i][j-1] - sumMatrix[i-1][j-1];
}
if (i1== 0 && j1 ==0)// start from row 0, column 0
if (i1== 0 && j1 ==0)// start from row 0, column 0
return sumMatrix[i2][j2];
else if ( i1 == 0) // start at row 0
return sumMatrix[i2][j2] - sumMatrix[i2][j1-1];
else if ( j1 == 0 ) // start at column 0
return sumMatrix[i2][j2] - sumMatrix[i1-1][j2];
else
return sumMatrix[i2][j2] - sumMatrix[i2][j1-1] - sumMatrix[i1-1][j2] + sumMatrix[i1-1][j1-1];
// A mini-window between Left and Right. Fixed Left Increment Right to adjust Window
// Sum all the value in row basis from left column to right column, get the number of row value
0 -2 - 7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
For the above matrix, the largest sum submatrix is:
9 2
-4 1
-1 8
2. Impelementation
3. Similar Ones
http://prismoskills.appspot.com/lessons/Dynamic_Programming/Chapter_07_-_Submatrix_with_largest_sum.jsp
// A mini-window between Left and Right. Fixed Left Increment Right to adjust Window
// Sum all the value in row basis from left column to right column, get the number of row value
0 -2 - 7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
For the above matrix, the largest sum submatrix is:
9 2
-4 1
-1 8
2. Impelementation
// Time:O(n^4), Space:O(n^2)
public static int getMaxMatrix(int[][] original)
{
// Important ! could be less than 0
int maxArea = Integer.MIN_VALUE;
int rowCount = original.length;
int columnCount = original[0].length;
int[][] matrix = precomputeMatrix(original);
for (int row1 =0; row1< rowCount; row1++ ){
for (int row2 = row1; row2 < rowCount; row2++){
for (int col1 = 0; col1 < colCount; col1++) {
for(int col2 = col1; col2 < colCount; col2++;) {
maxArea = Math.max(maxArea, computeSum(martix, row1, row2, col1,col2) );
}
}
}
}
}
private static int[][] preComputeMatrix(int[][] matrix)
{
// NOTE : every thing returned A NEW OBJECT
int[][] sumMatrix = new int[matrix.length][matrix[0].length];
for (int i = 0 ; i < matrix.length;i++){
for (int j = 0; j < matrix[0].length;j++){
if ( i==0 && j ==0 )
{
sumMatrix[i][j] = matrix[i][j];
}
else if ( j == 0 )
{
sumMatrix[i][j] = matrix[i][j] + sumMatrix[i-1][j];
}
else if ( i == 0 )
{
sumMatrix[i][j] = matrix[i][j] + sumMatrix[i][j-1];
}
else
{
sumMatrix[i][j] = matrix[i][j] + sumMatrix[i-1][j] + sumMatrix[i][j-1] - sumMatrix[i-1][j-1];
}
}
}
return sumMatrix;
}
private static int computeSum(int[][] matrix, int i1, int i2, int j1, int j2)
{
if (i1== 0 && j1 ==0)// start from row 0, column 0
return sumMatrix[i2][j2];
else if ( i1 == 0) // start at row 0
return sumMatrix[i2][j2] - sumMatrix[i2][j1-1];
else if ( j1 == 0 ) // start at column 0
return sumMatrix[i2][j2] - sumMatrix[i1-1][j2];
else
return sumMatrix[i2][j2] - sumMatrix[i2][j1-1] - sumMatrix[i1-1][j2] + sumMAtrix[i1-1][j1-1];
}
// Time:O(n^3)
// A mini-window between Left and Right. Fixed Left Increment Right to adjust Window
// Kadane's algorithm finds sub-array with maximum sum in O(n) for 1D arrays
public static int findMaxSum (int[][] matrix)
{
int maxSum=0;
int numCols = matrix[0].length;
int numRows = matrix.length;
for (int left = 0; left < numCols; left++)
{
int temp[numRows] = {0};
for (int right = left; right < numCols; right++)
{
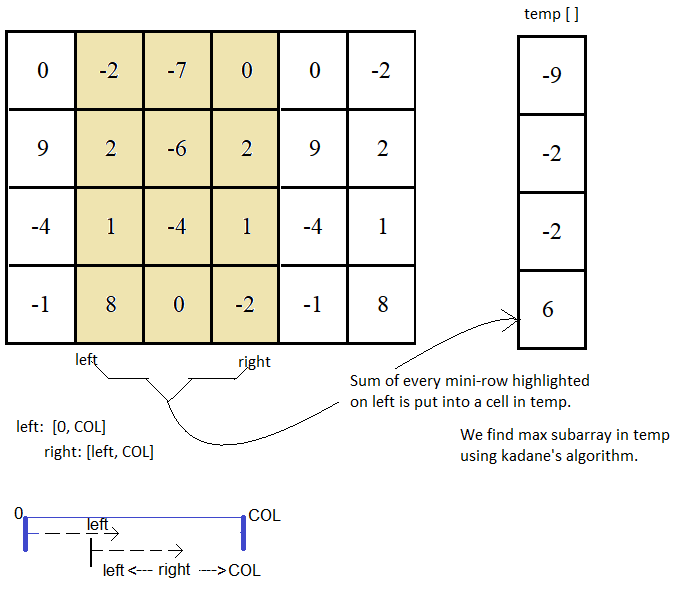
// Find sum of every mini-row between left and right columns and save it into temp[]
for (int i = 0; i < numRows; ++i)
temp[i] += matrix[i][right];
// Find the maximum sum subarray in temp[].
int sum = kadane(temp, numRows);
if (sum > maxSum)
maxSum = sum;
}
}
return maxSum;
}
http://prismoskills.appspot.com/lessons/Dynamic_Programming/Chapter_07_-_Submatrix_with_largest_sum.jsp
3. Similar Ones
http://prismoskills.appspot.com/lessons/Dynamic_Programming/Chapter_07_-_Submatrix_with_largest_sum.jsp
No comments:
Post a Comment